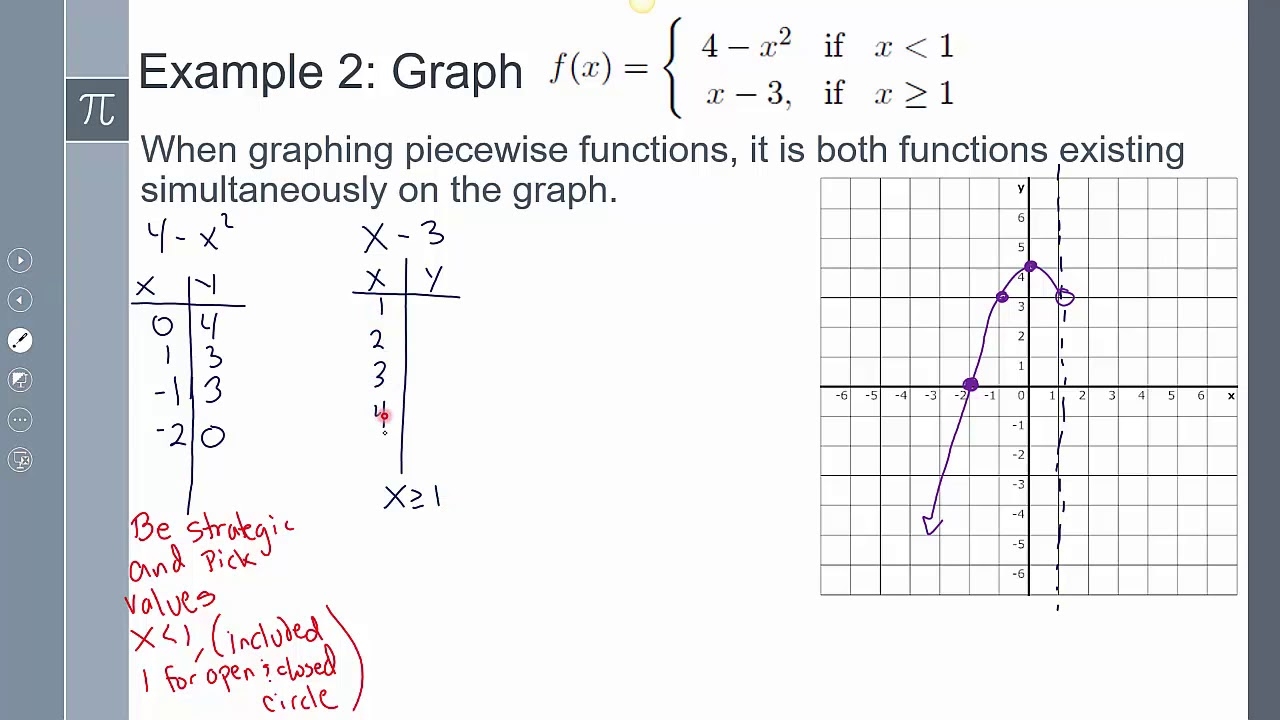
Graphing piecewise functions can be a challenging yet rewarding task for students learning about functions and their graphs. Piecewise functions are functions that have different rules or expressions for different parts of their domain. This type of function can be represented by multiple equations, each defined for a specific interval of the independent variable.
When graphing piecewise functions, it is important for students to understand how to identify the different parts of the function and plot them accurately on a coordinate plane. This helps in visualizing how the function behaves and how it transitions between different rules.
Graphing Piecewise Functions Worksheet
One way to practice graphing piecewise functions is through worksheets that provide various examples for students to work on. These worksheets typically include multiple exercises where students are given piecewise functions and are asked to graph them on a coordinate plane.
Students can start by identifying the different rules or expressions that make up the piecewise function. They can then plot each part separately on the graph, making sure to pay attention to any discontinuities or points of intersection between the different parts.
Additionally, students can practice analyzing the behavior of the function at specific points, such as finding the value of the function at a given x-coordinate or determining the domain and range of the function. This helps in developing a deeper understanding of how piecewise functions work and how they can be graphed effectively.
By working on graphing piecewise functions worksheets, students can improve their graphing skills and gain a better understanding of how functions can be represented and visualized. This type of practice can also help students prepare for more advanced topics in algebra and calculus where piecewise functions are commonly used.
In conclusion, graphing piecewise functions worksheets are a valuable resource for students to practice and master the skills needed to graph complex functions with multiple rules. By working through various examples and exercises, students can enhance their graphing abilities and deepen their understanding of how functions behave and transition between different parts of their domain.